Физика. Кравченко Н. Ю.
1.1. Кинематика материальной точки
Механическим движением будем называть любое изменение положения точки в пространстве.
Материальная точка — тело, размерами которого можно пренебречь. Иногда добавляют — «по сравнению с расстоянием до этого тела».
Система отсчета — это совокупность трех понятий: точки отсчета, системы координат и прибора для измерения времени. Точкой отсчета может стать все, что угодно, любая точка в пространстве, как неподвижная, так и движущаяся.
Система координат предназначена для того, чтобы можно было абсолютно однозначно определить положение любой точки в пространстве. Некоторые из них: зональная система координат, система координат Гаусса — Крюгера, полярная, прямоугольная, сферическая, цилиндрическая (рис. 1.1).
Рис. 1.1. Системы координат:
а) сферическая, б) цилиндрическая, в) декартова левосторонняя, г) декартова правосторонняя
Пример: считаем, что большой палец показывает направление оси 0x, указательный — направление 0y, средний — 0z. Получим правостороннюю декартову систему координат, а правило, которым ее определили, называют «правилом правой руки» (рис. 1.2).
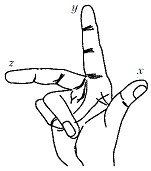
Рис. 1.2. Правило правой руки
Прямолинейное движение — движение по прямой линии.
Криволинейное движение — движение не по прямой. Необходимо заметить, что любое криволинейное движение можно представить как совокупность двух типов движения — прямолинейного и по окружностям разного радиуса.
Равномерное движение — движение с постоянной скоростью.
Переменное движение — движение, при котором ускорение точки отлично от нуля a ≠ 0. Но если a = const, то движение называют равнопеременным. При этом ускорение может быть как положительным, и такое движение называется равноускоренным, так и отрицательным, такое движение — равнозамедленное.
Скорость — это понятие уже более широкое, нежели предыдущие, разберем его более детально. Средняя скорость — путь, отнесенный к интервалу времени, за который этот путь пройден.
Пример: автомобиль движется из города Б в город В и расстояние в 300 км преодолевает за 4 часа. Это значит, что его средняя скорость
Но в дороге были сделаны две остановки. Значит, скорость не всегда была равна 75 км/ч. Могло даже быть так, что скорость вообще нигде не была равна 75 км/ч. В данном случае речь идет о средней скорости.
Из классического определения производной мгновенная скорость есть
Из этого уравнения можно выразить путь
Геометрический смысл пути: путь s численно равен площади фигуры S, ограниченной кривой v(t) между точками 1 и 2 (рис. 1.3).
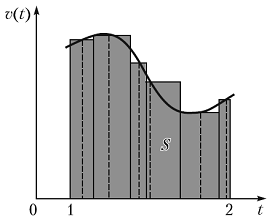
Рис. 1.3. Геометрический смысл пути
Ускорение
- Среднее ускорение — изменение скорости за интервал времени
.
- Мгновенное ускорение — первая производная скорости по времени, либо вторая производная перемещения по времени
.
Уравнение движения
(1.1)
В скоростях
(1.2)
Уравнения (1.1) и (1.2) называют уравнениями движения материальной точки. Знак «» перед ускорением говорит о его направлении. Если тело движется без ускорения, т.е. a = 0, то уравнение (1.1) преобразуется к виду: x = x0 + v0t. Уравнения (1.1) и (1.2) могут быть применены только к случаю прямолинейного движения. Для описания движения тела по окружности используют уравнения вращательного движения
В этой системе φ — угловое перемещение, — угловая скорость,
— угловое ускорение. Направление угловой скорости ω определяется правилом правого винта: если вкручивать винт с правой резьбой, направление его поступательного движения совпадет с направлением угловой скорости (рис. 1.4).
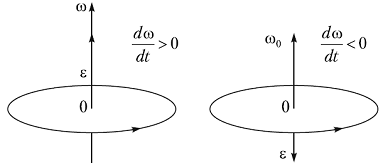
Рис. 1.4. Угловая скорость ω и угловое ускорение ε
Полное ускорение
, где an — нормальное (или центростремительное) ускорение, aτ — тангенциальное ускорение точки (рис. 1.5).
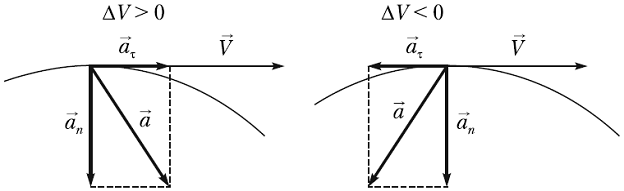
Рис. 1.5. Нормальное и тангенциальное ускорения
Связь линейных и угловых величин
Важно отметить
Уравнения движения (1.1) и (1.2) не учитывают массу тела.
Важно запомнить
- Уравнение движения:
- Полное ускорение:
;
- Связь линейных и угловых величин:
