Физика. Кравченко Н. Ю.

Для описания вращательного движения удобнее использовать величины, направления которых не зависят от точки приложения.

Моментом силы (или вращающим моментом, , рис. 1.7) называется векторное произведение радиус-вектора (или плеча силы) на саму силу

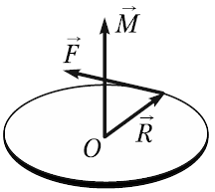
Рис. 1.7. Направление вращающего момента

Векторное произведение двух перпендикулярных векторов: чтобы определить направление момента сил , нужно знать правило «правой тройки векторов» или «правило правой руки» (рис. 1.8).

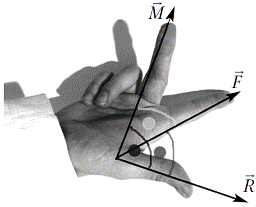
Рис. 1.8. Правило правой руки

 

Векторное произведение двух произвольных векторов: при перемножении непараллельных векторов  и  нужно один из них (например, ) разложить на две компоненты и затем векторно перемножить    способом, описанным выше. При этом должно выполняться условие:

Момент импульса

где  — импульс тела,  — радиус-вектор. Направление момента импульса  определяется правилом правой тройки векторов (правой руки). Скалярное выражение для момента импульса

В последнем уравнении вводится новая для нас физическая величина, момент инерции.

Момент инерции

.

2-й закон динамики для вращательного движения выражается из дифференциальной формы 2-го закона Ньютона , с учетом выражения (1.5) для момента силы

 

Таким образом, вращающий момент равен скорости изменения момента импульса.

Закон сохранения момента импульса. Если L = const, то производная от него равна нулю, т.е. M = 0. Физически это означает, что если момент внешних сил относительно неподвижной точки равен нулю (M = 0), то момент импульса сохраняется (L = const).

Моменты инерции некоторых тел

Сплошной однородный цилиндр

Бесконечно тонкий диск. Отметим, что диск — это тот же цилиндр, но меньшей высоты, тогда

.

где l — длина стержня. Момент инерции относительно оси, проходящей через край стержня (рис. 1.9)

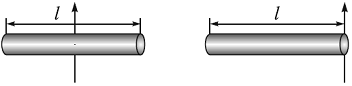
Рис. 1.9. Геометрия тонкого стержня при определении его моментов инерции

Однородная прямоугольная пластина

относительно оси 0x: , относительно оси 0y: .

Прямоугольный параллелепипед

Теорема Гюйгенса-Штейнера: момент инерции тела относительно произвольной оси I_a равен сумме моментов инерции относительно параллельной оси, проходящей через центр масс (I₀) и ma², где a — расстояние между осями. Таким образом,

.

Кинетическая энергия вращающегося тела складывается из двух компонент: кинетической энергии поступательного движения и кинетической энергии движения вращательного.

С учетом выражения (1.6) можно записать

Работа при вращении

Мощность при вращении

Трехмерное вращение: примером является гироскоп. Гироскопом называют массивное быстро вращающееся тело с незакрепленной осью вращения (рис. 1.10).

Рис. 1.10. Трехмерный гироскоп

Свойства гироскопа:

• ось гироскопа сохраняет свое положение в пространстве неизменным;
• прецессия оси гироскопа.