Физика. Кравченко Н. Ю.

Механика: основные принципы и понятия

1.1. Кинематика материальной точки

Пример решения задачи

Дано: снаряд вылетел из орудия под углом α к горизонту с начальной скоростью v0. Определить максимальную высоту подъема этого снаряда и дальность его полета.

Решение: запишем уравнения движения в виде

Поскольку движение снаряда происходит в двумерной плоскости, распишем проекции уравнений движения на горизонтальную и вертикальную оси.

	(1)
	(2)
	(3)

В этих уравнениях l — искомая дальность полета, h — искомая высота полета, t — полное время полета, t₁ = t/2 — время полета до середины пути, где снаряд достигает максимума высоты. Из (1.3) выражаем время t₁

	(4)
	(5)

Подставляем (4) в (2), а (5) в (1) и получаем

Пример решения задачи

Дано:

Материальная точка движется так, что ее ускорение задается выражением a= kt, где k = const. Через время t₁ = 1 c ускорение становится равным a₁ = 2 м/с². Определить скорость v₂ и пройденный путь s₂ материальной точки к моменту времени t₂ = 10 c.

Решение:

Определим скорость точки как .          (П.1)

Из условия следует, что .         (П.2)

Подстановка (П.2) в (П.1) дает .

Путь определим как .

Для момента времени t₂ путь.

Подстановка числовых значений дает результаты: v₂ = 100 м/с, s₂ = 333,3 м/с².

1.2. Динамика материальной точки

Пример решения задачи

Дано: два бруска c массами m₁ и m₂ соединены нерастяжимой нитью и перекинуты через невесомый блок так, как показано на далее рисунке. Коэффициент трения между вторым бруском и поверхностью — k, угол наклона поверхности — α. Определить, куда и с каким ускорением a будут двигаться бруски. Найти силу натяжения нити T.

Решение: на рисунке изображены направления всех сил, действующих на бруски. Запишем второй закон Ньютона для обоих брусков на направления их движения. При этом предположим, что система будет двигаться в сторону первого бруска (т.е., ускорение направлено налево). Если последнее неверно, то в ответе мы получим отрицательное ускорение.

	(1)
	(2)

Кроме того, силу трения можно выразить как

(3)

Из (1) выразим T и подставим в (2). Из (3) F_тр также подставим в (2).

	(4)
	(5)

Раскрываем скобки в (5) и выражаем ускорение a

(6)

В (4) подставляем (6)

.

Направление ускорения будет зависеть от числового значения знаменателя в выражении (6) и совпадет с выбранным нами направлением в случае, если .

Пример: движение тела в поле силы тяжести Земли

Рассмотрим падение тела в поле силы тяжести. В этом случае, согласно 2-му закону Ньютона, . В предыдущей главе мы уже говорили об уравнении движения . Подставим это уравнение во 2-й закон Ньютона и учтем, что a = g:

.

Получилось верное равенство. Из математики вам, наверное, известно, что решением уравнения является такая функция, которая при подстановке в это уравнение дает верное равенство. Что мы и получили.

Пример решения задачи

Дано:

Брусок скользит вдоль наклонной плоскости (см. рисунок ниже). Угол наклона плоскости равен α = 30^o, коэффициент трения между бруском и плоскостью k = 0,3. Определить, за какое время t брусок пройдет вторую половину своего пути, если весь путь равен l = 5 м.

Решение:

Второй закон Ньютона в проекциях на оси дает выражения:

Тут мы учли, что сила трения F_тр = kN.

Из полученных уравнений выражаем ускорение

.

Поскольку , то время прохождения бруском всей плоскости целиком есть

.

Время, затраченное на прохождение первой половины пути, есть

, а искомое нами время определяем как

Подстановка числовых значений дает t = 0,59 c.

 

Пример решения задачи

Дано:

Ракета поднимается вертикально вверх с нулевой начальной скоростью. Начальная масса ракеты — m₀. Запишите уравнение зависимости скорости ракеты v от ее массы m и времени t. Для простоты считать поле тяготения Земли однородным и сопротивление воздуха не учитывать.

Решение:

Запишем уравнение Мещерского в виде: , где u — скорость истечения газов относительно ракеты, она противоположна направлению скорости ракеты v.

Преобразуем последнее выражение к виду

, откуда следует

1.3. Работа и энергия

Рассмотрим пример

Вы подняли с земли большой камень и перенесли его из точки А в точку В. При этом у вас нет никаких сомнений, что вашей физической силой совершена некоторая работа. Затем вы вернули камень в начальную точку А. Какую итоговую работу совершила ваша сила? Вам кажется, что существенную, а на самом деле — нулевую. Почему? Ответ очень прост. Когда вы подняли камень, то ваша сила совершила некоторую работу +A, когда перемещали камень в точку В и обратно, работа не совершалась (согласно выражению (1.3), если cosα = 0, следовательно, работа не совершается силой перпендикулярно ее направлению), когда опускали камень обратно в точку А, то работу совершала не ваша сила, а сила тяжести, ее значение –A. Итоговая работа вашей силы .

Докажем закон сохранения механической энергии, используя 2-й закон Ньютона. Если кинетическая энергия тела меняется во времени, то можно записать

(1)

Мы получили, что изменение кинетической энергии во времени есть мощность силы.

Теперь рассмотрим падение тела в поле силы тяжести Земли, где F = mg. Согласно уравнению мощности, для силы тяжести при перемещении тела будет выполняться

(2)

Теперь мы получили, что мощность силы есть изменение потенциальной энергии. Следовательно, уравнения (1) и (2) выражают одно и то же. Итак, мы доказали, что изменение кинетической энергии равно изменению потенциальной энергии. А это и означает, что полная механическая энергия сохраняется

.

Пример: движение планеты вокруг Солнца

В предыдущем примере сила тяжести F = mg была величиной постоянной. А если F ≠ const, будет ли тогда выполняться закон сохранения энергии?

Давайте рассмотрим движение планеты вокруг Cолнца. Изменение кинетической энергии есть интеграл от работы силы тяготения, т.е.

.

Получили выражение для изменения потенциальной энергии. То есть, изменение кинетической энергии равно изменению энергии потенциальной. Таким образом, и для сил, не являющихся постоянными во времени, закон сохранения механической энергии также выполняется.

Пример решения задачи

Дано: камень, брошенный горизонтально с высоты h без начальной скорости, падает на землю. При этом потери на преодоление сопротивления воздуха составляют 20% энергии камня. Определить скорость падения камня на землю.

Решение: первый способ — применим уравнения движения (1.1 — 1.2) в проекции на вертикальную ось. Проекция на горизонтальную ось нас в данном случае не интересует.

.

Последнее выражение известно как формула Торричелли. Потери 20% энергии говорят о том, что величина потенциальной энергии была в 1,25 раза больше, чем мы рассматриваем. Поскольку высота h и потенциальная энергия mgh связаны линейно, то справедливо будет записать

.

Второй способ — применим для решения закона сохранения механической энергии

.

В последнем уравнении мы учли потери 20% энергии, т.е. только 80% потенциальной энергии перешли в кинетическую, остальная — ушла на преодоление трения. Сократив массу, получим

.

1.4. Вращательное движение тел

Для демонстрации закона сохранения момента импульса рассмотрим пример

Все мы восхищаемся вращением фигуристов на льду или балерин на сцене. Раскинув руки в стороны, балерина замедляет угловую скорость своего вращения, прижав к себе, наоборот, резко увеличивает угловую скорость (см. рисунок далее) А секрет трюка очень прост. Если закон сохранения момента импульса справедлив, то . Следовательно, меняя величину плеча (R), можно получить квадратичное изменение угловой скорости (ω). Что мы и наблюдаем.

Пример решения задачи

Дано: определить момент инерции сплошного однородного цилиндра массой m относительно горизонтальной оси (см. рисунок ниже). Радиус основания цилиндра R.

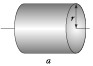
Решение: если цилиндр сплошной и однородный, то для любого сечения будет справедливым равенство

.

Тогда получим

,

где s — площадь основания цилиндра, ; R — радиус цилиндра (не путайте с r — текущей координатой точки). Остается лишь понять ход дальнейших преобразований:

.

Окончательно получили, что момент инерции цилиндра относительно горизонтальной оси равен

.

Пример

Необходимо рассчитать момент инерции шара относительно оси, касательной к его поверхности. Воспользуемся теоремой. Момент инерции шара относительно оси, проходящей через центр масс, равен . Расстояние между осью, проходящей через центр шара, и нашей касательной осью a = R. Тогда

.

И никаких громоздких вычислений.

Простейшим примером гироскопа является обычный детский «волчок» (см. рисунок ниже). С его помощью мы и разберем причины возникновения прецессии. Со стороны Земли на «волчок» действует сила тяжести (mg), приложенная к центру масс. Плечо силы есть L. Вращающий момент выражается векторным произведением

.

Направление вращающего момента определяется правилом правой руки.

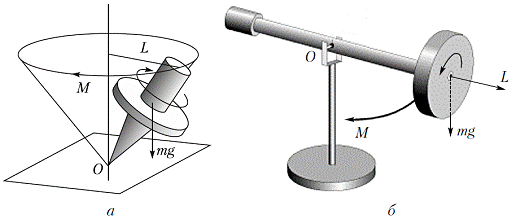
Простейшие гироскопы

1.5. Гравитационные силы. Силы инерции

Пример

Представьте, что из некоторой точки над поверхностью Земли мы одновременно запустили два тела: первое — вертикально вниз без начальной скорости, второе — горизонтально с некоторой начальной скоростью. За первую секунду тело № 1 пройдет 4,9 м (это легко рассчитать из уравнения движения), следовательно, приблизится к Земле на 4,9 м. Тело № 2 за первую секунду в горизонтальном направлении может пройти какой угодно путь, в зависимости от горизонтальной скорости, а вот в вертикальном направлении — «упадет» на те же 4,9 м. Если вы верите в то, что Земля не стоит на трех слонах и является сферой, то понимаете, что за счет кривизны поверхности Земли, тело № 2 в результате падения приближается к Земле на 4,9 м в направлении оси y, но, тем не менее, в направлении оси x может от нее отдалиться. В результате, итоговая высота такого падающего тела может не только не уменьшиться, но, наоборот, даже увеличиться.

Так что теперь вы тоже знаете, что и Луна «падает» на Землю, и Земля «падает» на Солнце, и яблоко падает на голову по одному и тому же закону.

Маятник Фуко. Действие силы Кориолиса можно наблюдать на примере маятника Фуко. Знаменитый опыт французский физик Фуко провел в Парижском Пантеоне в 1851 г. Основной целью опыта было желание доказать, что Земля вращается вокруг своей оси.

Маятник представлял собой шар массой 28 кг, подвешенный под куполом на проволоке длиной 67 м (см. рисунок далее). При освобождении маятника он начинал качаться. Под маятником было сделано круговое ограждение радиусом 6 м с центром под точкой подвеса. На ограждение насыпан песок, чтобы при каждом качании металлическое острие, прикрепленное к шару снизу, могло сметать его на своем пути. Маятник такой длины совершает одно полное колебание за 16,4 с, и вскоре стало видно, что плоскость качания маятника поворачивается по часовой стрелке относительно пола. За час плоскость качания повернулась более чем на 11°, а за 32 ч совершила полный оборот и вернулась в прежнее положение. Эта впечатляющая демонстрация приводила зрителей в восторг, им казалось, что они чувствуют вращение Земли под ногами.

Маятник Фуко в Парижском Пантеоне

Движение тел вблизи поверхности Земли. Есть и другие проявления действия силы Кориолиса, правда, не такие эффектные, как в опыте Фуко.

Например

При свободном падении тела отклоняются к востоку (в северном полушарии) или к западу (в южном полушарии). Снаряд, движущийся на север, кориолисова сила заставляет отклоняться к востоку (в северном полушарии). Тело, движущееся вдоль экватора на восток, поднимается кверху. А тело, движущееся вдоль меридиана, сила Кориолиса отклоняет вправо (см. рисунок далее).

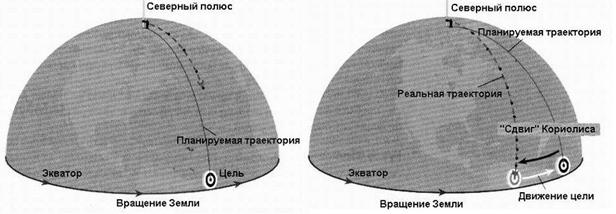
Движение тел вблизи поверхности Земли

Направление силы, напомню, определяется векторным соотношением (1.9) и правилом «правой тройки векторов».

Аналитические задания по лекции 1

1. Подумайте над решением задачи Льюиса Кэрролла: «Через блок переброшена веревка, на одном ее конце висит груз, за другой конец держится обезьяна. Вес обезьяны равен весу груза. Как будет двигаться груз, если обезьяна полезет наверх?» (рисунок далее).

Задача Л. Кэрролла

2. Где на Земле тела легче всего? Вопрос этот похож на загадку-шутку. Но, если подумать, то на него можно дать вполне обоснованный ответ. Какой?
3. Вам хорошо известен закон сохранения массы. А теперь представьте себе клетку, в которой сидит птичка, а сама клетка находится на весах. Порассуждайте, изменятся ли показания весов, если птичка взлетит и будет летать по клетке? Обоснуйте свои рассуждения.
4. Объясните с физической точки зрения смену времен года. Помогут ли вам в рассуждениях законы Кеплера?
5. Известно, что южное полушарие Земли летом получает от Солнца тепла на 7% больше, чем северное полушарие летом (через 6 мес.). Почему?
6. Помните знаменитую скороговорку «Ехал Грека через реку...»? А вот вам похожая задачка:

Плыл Грека массой M длиною L

И рак его за время τ съел.

Сперва была им съедена навеки

Рука длиною p% Греки.

На обе рак затратил у реки

 времени обеда.

Вес Греки равен силе Архимеда.

Определить диаметр руки.